信号也分 “规律党” 和 “随性派”?周期VS非周期信号
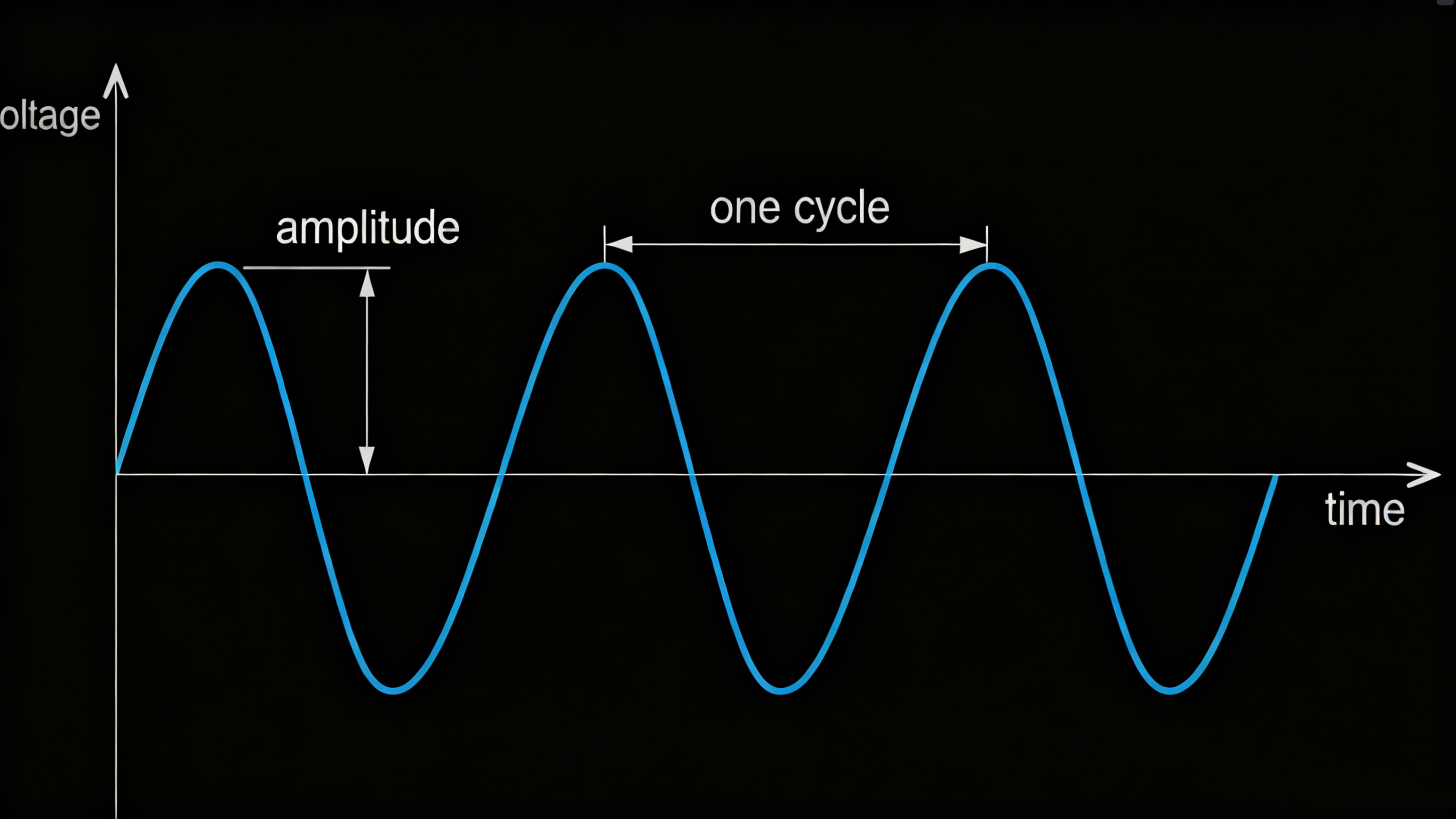
通信的基础是被称为正弦波的模拟信号,如图所示。正弦波之所以重要,不仅因为它们在各种情况下都能自然出现,还因为它们的数学运算简单。下图显示的是一个正弦变化的电压,但其他属性,例如电流、功率、压力等等,也可以以这种方式变化。
二、周期信号的定义
周期信号 ( Periodic signal) 是指以固定时间间隔重复的信号。周期信号可以表示为频率为信号基频整数倍的正弦函数之和。周期信号的基频是信号中存在的最低频率。
周期信号的特征在于其周期(即信号重复所需的时间)和频率(即信号在给定时间段内经历的循环次数)。周期信号中两个连续最大值(或任何其他对应点)之间的部分称为一个周期。一个周期的持续时间称为周期。一秒钟内的周期数称为频率。频率的单位是赫兹 (Hz),其中 1 Hz = 每秒 1 个周期。设 f 为频率(单位为赫兹),T 为周期(单位为秒),则:
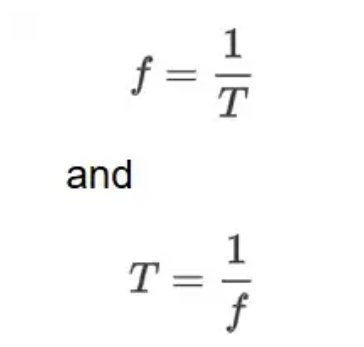
三、周期信号频谱的特点是什么?
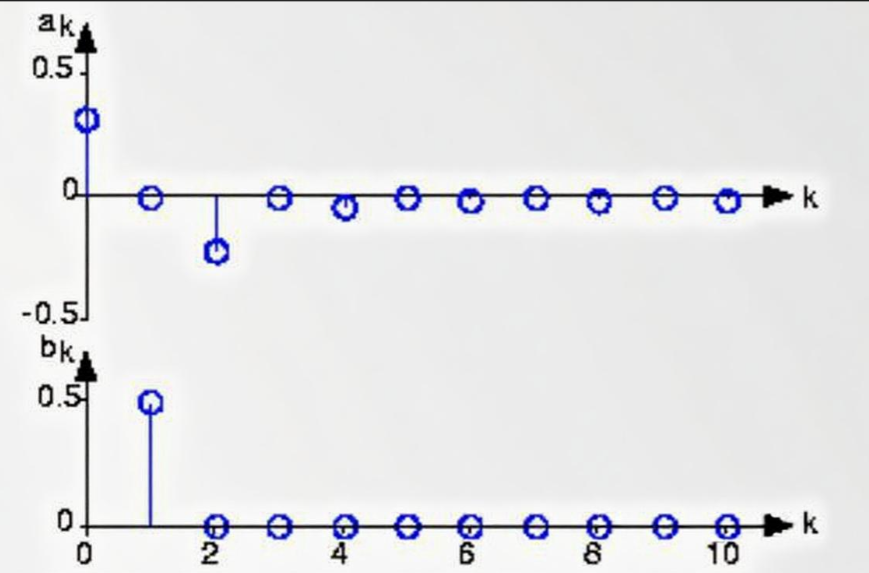
周期信号(例如半波整流正弦波)由一系列基本正弦波组成。傅里叶系数随频率指数变化的函数图(如图所示)显示了信号的频谱。
“频谱”一词意味着独立变量(此处为 k)以某种方式与频率相对应。每个系数都与频率为 k/T 的正弦波直接相关。因此,如果我们对 1 kHz 正弦波进行半波整流,k=1 对应 1 kHz,k=2 对应 2 kHz,等等。
傅里叶频谱的一个微妙但非常重要的方面是它的唯一性:你可以从信号(分解)中找到频谱,也可以从频谱(合成)中找到信号。因此,信号的任何方面都可以从频谱中找到,反之亦然。信号的频域表达是其频谱。周期信号可以在时域(作为函数)或频域(作为频谱)中定义。
四、周期信号有哪些类型?
正弦波
正弦波是一种以恒定时间间隔重复出现的波形,其形状为正弦波,如下图所示。它是电子工业通信电路中最常用的信号。
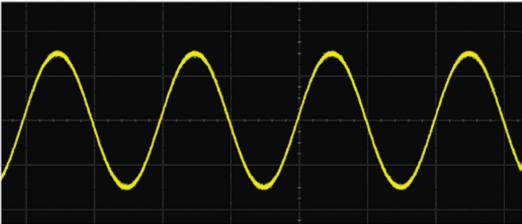
方波
它是一种以恒定时间间隔重复出现的波形,形状为均匀的正方形,如下图所示。它是电子工业电路设计和分析中最常用的信号。
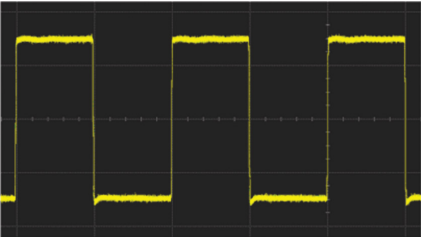
三角波
它是一种以恒定时间间隔重复出现的波形,形状为均匀的三角形,如下图所示。它是电子工业DC-DC转换器电路中最常用的信号。
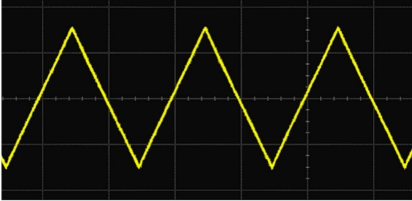
锯齿波
锯齿波是一种以固定时间间隔重复出现的波形,形状呈锯齿状。它是减法模拟和虚拟模拟音乐合成器中最常见的信号,用于产生声音。
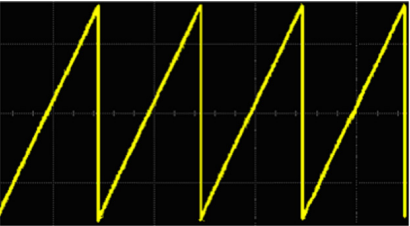
五、周期信号的特点
· 周期信号的一个重要性质是其周期性。周期信号之所以具有此性质,是因为它们在一段称为“周期”的恒定时间间隔后呈现出重复的模式。
· 周期信号的另一个重要性质是振幅。它是信号的最大绝对值,表示信号的幅度或强度。
· 我们可以将周期信号的频率定义为单位时间内的周期数。它是时间周期的倒数,以赫兹为单位。
· 周期信号的方向、形状或形态是另一个重要性质。常见的周期波形包括正弦波、方波、锯齿波和三角波。
六、什么是非周期信号?
通信的本质在于传递信息。然而,周期信号由于其可预测性,其信息传递的可能性有限。在接收到几个周期并确定其模式后,我们知道接下来的周期将完全相同。信号在开始时可能传达重要信息,例如火警警报,一旦听到声音就会立即采取行动。但是,如果信号的幅度、频率、相位或任何其他方面都保持不变,则几乎无法向接收者传递任何进一步的信息。因此,在实际通信中,完全周期性信号是例外。承载真实信息(例如语音、音乐或视频)的信号不会无限重复。
非周期信号(也称为非周期信号)与周期信号不同,它们不只有一个特定的频率。相反,它们分布在一个连续的频率范围内。例如,语音信号的频率范围从大约100 Hz到几千Hz(对于电话质量的语音,通常假设其频率范围为300 Hz到3400 Hz)。
七、非周期信号的定义
非周期信号 ( Non-periodic signal )是指不以固定间隔重复的信号。这意味着它没有基频,其频谱通常不由离散频率组成。非周期信号可以是连续的,也可以是离散的,可以是确定性的,也可以是随机的。非周期信号的例子包括白噪声、脉冲和任意波形。非周期信号在实际应用中很常见,例如语音、音乐和环境噪声。
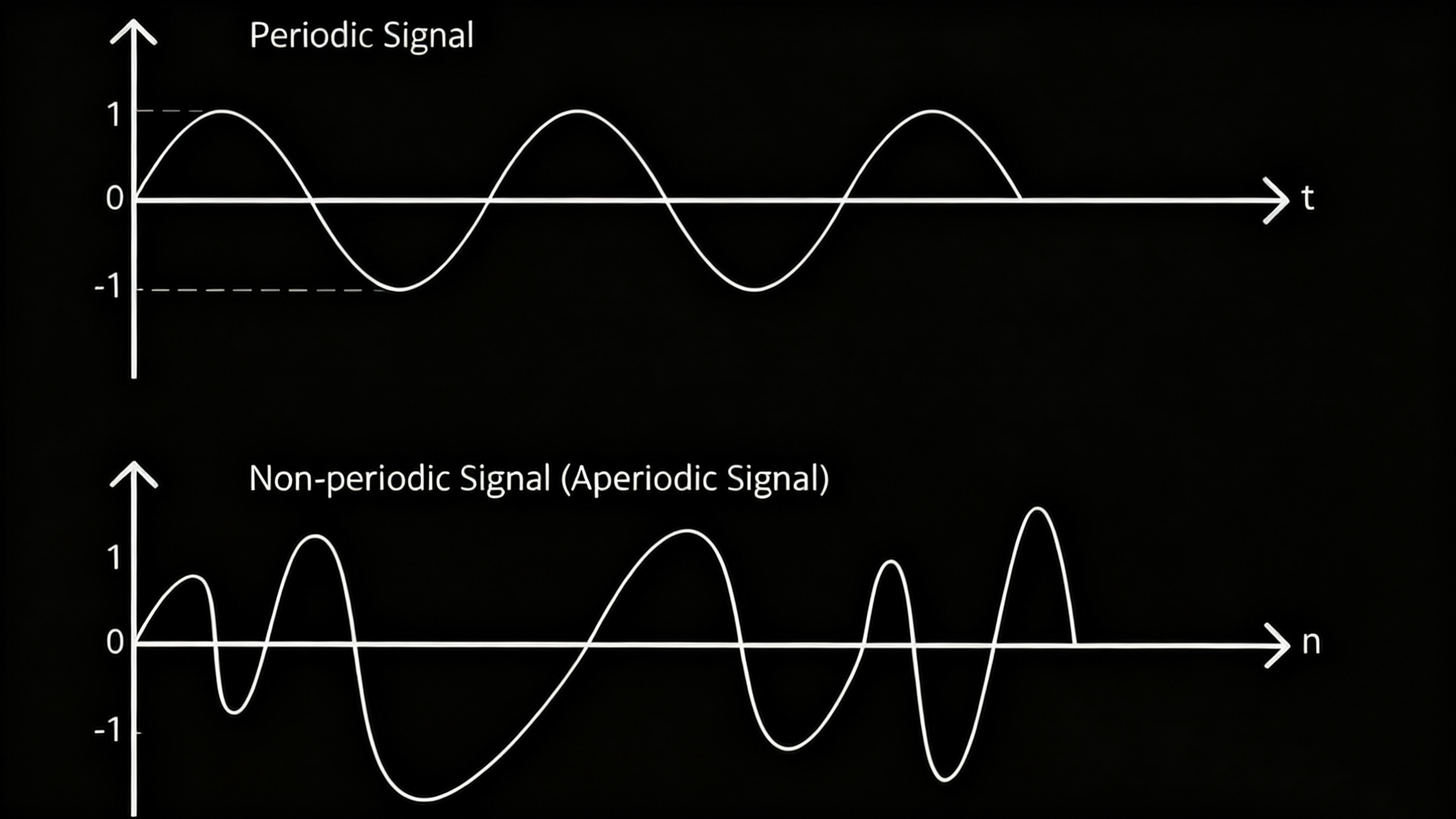
非周期信号的频谱具有连续性、无限性和频谱密度三个核心特点。这些特性使其在频域分析与周期信号形成显著差异,具体表现为频谱连续覆盖所有频率、范围无限延伸,以及能量通过密度形式分布。
1. 频谱的连续性
非周期信号的频谱在频域上是连续分布的,这与周期信号离散的谱线结构不同。由于信号没有周期性重复,其频率成分不会集中在基频整数倍的离散点上,而是以连续函数形式覆盖从低频到高频的所有频率。例如,非周期矩形脉冲的频谱呈现为连续的sinc函数形状,而非离散的谱线。
2. 频谱范围的无限性
理论上,非周期信号的频谱范围可以延伸至无限高频率。这是因为信号在时域上的非周期性导致频域中需要无限多的频率分量来精确描述其变化。然而,实际应用中大部分能量集中在有限带宽内(如矩形脉冲的主瓣带宽),高频成分的幅度随频率升高逐渐衰减,但不会完全消失。
3. 频谱密度的能量描述方式
非周期信号的能量或幅度通过频谱密度函数(如傅里叶变换的幅度谱)表征。频谱密度表示单位频率范围内的能量分布,而非离散频率点的能量值。例如,矩形脉冲的频谱密度随频率升高呈振荡衰减趋势,这说明高频成分的能量密度逐渐降低,但所有频率成分共同构成完整的信号时域波形。
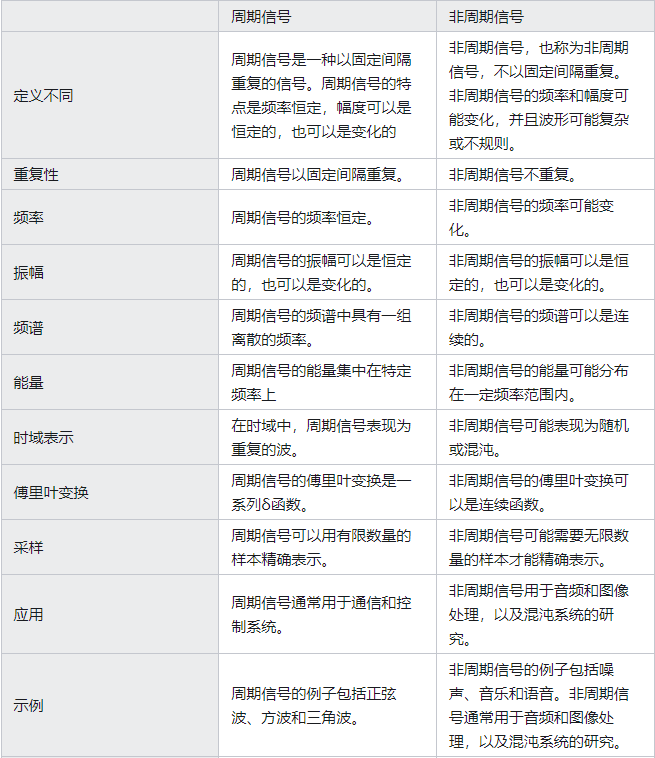
九、周期信号和非周期信号的比较